Abstract
How likely is it that a sum of rounded values is not identical to their rounded sum?
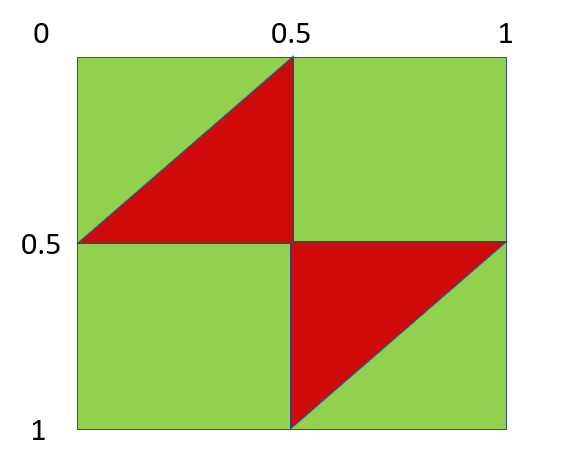
For two random floating point numbers this is obvious: The likelihood is around 25% - that is the percentage of red in this picture:
But it might be somewhat surprising that the likelihood approaches 90% if you round and add more and more numbers:
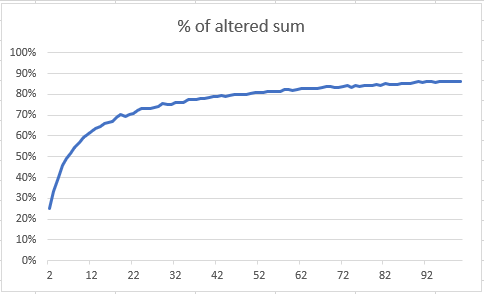
With seven floating point numbers the likelihood is already larger than 50% that the sum of rounded values is not equal to their rounded sum.
How can you fix this issue? Use RoundToSum.
Rounded Percentages
Rounded percentages also often fail to add up to 100%.
With two random numbers we do not face a big issue:
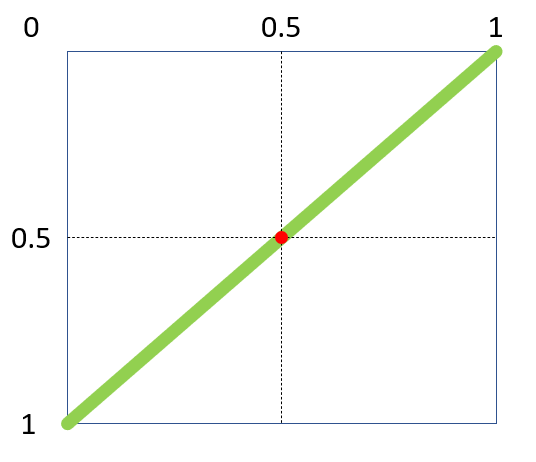
But with more random numbers it is similar to the problem stated initially, just with around one number more. Rounded percentages of three arbitrary numbers fail to add up to 1 with a chance of around 25%:
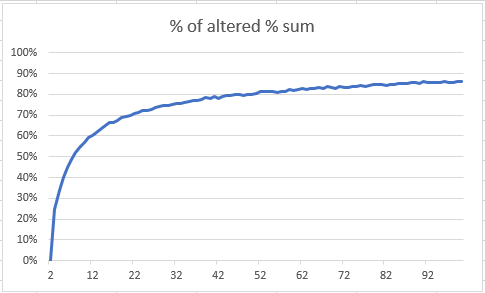
Here with eight random numbers the likelihood is larger than 50% that the rounded percentages do not add up to 1.
Again: with RoundToSum you can fix this.
Literature
Diaconis, P., & Freedman, D. (13. Juli 2007). (Externer Link!) On Rounding Percentages.
Frederick Mosteller, Cleo Youtz, Douglas Zahn (Demography, 1969, 4, 850-858). The Distribution of Sums of Rounded Percentages.
Example of Use
MrExcel.com (External link!) Allocation (Rounding Issue)
Appendix – Monte Carlo Program Codes
Please read my Disclaimer.
Option Explicit
Const n = 100
Const runs = 20000
Const bOnlyPositive = True 'Without loss of generality
Sub monte_carlo_add_rounded_values()
'Calculates for 2 to n how likely it is
'that rounding would not alter their sum.
'Example: for 2 numbers there is a 25% chance
'that the sum of their rounded values is not
'equal to their rounded sum.
'Source (EN): https://www.sulprobil.com/rounding_values_alters_their_sum_en/
'Source (DE): https://www.bplumhoff.de/werte_runden_aendert_ihre_summe_de/
'(C) (P) by Bernd Plumhoff 16-Dec-2023 PB V0.3
Dim i As Long
Dim j As Long
Dim k As Long
Dim m As Long
Dim d As Double
Dim s1 As Double
Dim s2 As Double
With Application.WorksheetFunction
Randomize
For i = 2 To n
m = 0
For j = 1 To runs
s1 = 0#
s2 = 0#
For k = 1 To i
If bOnlyPositive Then
d = Rnd()
Else
d = 2# * Rnd() - 1#
End If
s1 = s1 + d
s2 = s2 + .Round(d, 0)
Next k
s1 = .Round(s1, 0)
If s1 <> s2 Then
m = m + 1
End If
Next j
Cells(i, 1) = i
Cells(i, 2) = m / runs
Next i
End With
End Sub
Sub monte_carlo_percentage_sum_of_rounded_values()
'Calculates for 2 to n how likely it is that
'rounding would not alter their percentage sum.
'Example: for 2 numbers there is a 25% chance
'that the sum of their rounded values is not
'equal to their rounded sum.
'Source (EN): https://www.sulprobil.com/rounding_values_alters_their_sum_en/
'Source (DE): https://www.bplumhoff.de/werte_runden_aendert_ihre_summe_de/
'(C) (P) by Bernd Plumhoff 16-Dec-2023 PB V0.2
Dim i As Long
Dim j As Long
Dim k As Long
Dim m As Long
Dim s1 As Double
Dim s2 As Double
With Application.WorksheetFunction
Randomize
For i = 2 To n
m = 0
ReDim e(1 To i) As Double
For j = 1 To runs
s1 = 0#
For k = 1 To i
If bOnlyPositive Then
e(k) = Rnd()
Else
e(k) = 2# * Rnd() - 1#
End If
s1 = s1 + e(k)
Next k
s2 = 0#
For k = 1 To i
e(k) = .Round(1000# * e(k) / s1, 0)
s2 = s2 + e(k)
Next k
If s2 <> 1000# Then
m = m + 1
End If
Next j
Cells(i, 1) = i
Cells(i, 2) = m / runs
Next i
End With
End Sub
Download
Please read my Disclaimer.
How_likely_does_rounding_values_alter_their_rounded_sum.xlsm [43 KB Excel file, open and use at your own risk]