Abstract
With an explicit form of a cumulative distribution function inverse you should use sbRandCDFInv but if there is no such one then you can apply a linear approximation with the probability distribution function sbRandPDF. Unfortunately the sbRandPDF approach is computationally quite expensive, even if you reduce the number of linear points in case of identical or almost identical slopes.
A stratified sample:
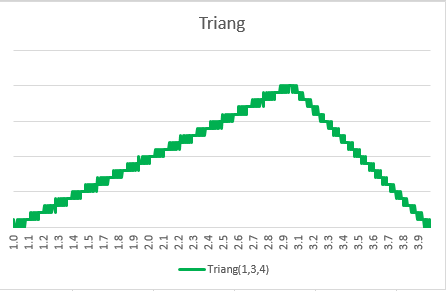
Appendix – sbRandPDF Code
Please note that this function needs (calls) sbRandGeneral.
Please read my Disclaimer.
Option Explicit
Function sbRandPDF(Optional dParam1, Optional dParam2, _
Optional dParam3, Optional dRandom = 1#) As Double
'Source (EN): http://www.sulprobil.com/sbrandpdf_en/
'Source (DE): http://www.bplumhoff.de/sbrandpdf_de/
'(C) (P) by Bernd Plumhoff 12-Sep-2014 PB V0.15
Dim dRand As Double
Dim i As Long
Static dPar1 As Double
Static dPar2 As Double
Static dPar3 As Double
Static vX(0 To 1000) As Variant
Static vY(0 To 1000) As Variant
If dRandom < 0# Or dRandom > 1# Then
sbRandPDF = CVErr(xlErrValue)
Exit Function
End If
If dRandom = 1# Then
dRand = Rnd()
Else
dRand = dRandom
End If
If dParam1 <> dPar1 Or dParam2 <> dPar2 Or dParam3 <> dPar3 Then
dPar1 = dParam1
dPar2 = dParam2
dPar3 = dParam3
'Initialize RandGeneral call parameters
For i = 0 To 1000
vX(i) = dPar1 + i * (dPar3 - dPar1) / 1000#
'Now we can insert an arbitrary PDF function
If vX(i) < dPar2 Then
vY(i) = (vX(i) - dPar1) / ((dPar3 - dPar1) * (dPar2 - dPar1))
If vY(i) < 0# Then vY(i) = 0#
Else
vY(i) = (dPar3 - vX(i)) / ((dPar3 - dPar1) * (dPar3 - dPar2))
If vY(i) < 0# Then vY(i) = 0#
End If
Next i
End If
'Depending on the PDF input range you need to feed start
'and end values to sbRandGeneral
sbRandPDF = sbRandGeneral(dPar1, dPar3, vX, vY, dRand)
End Function