Abstract
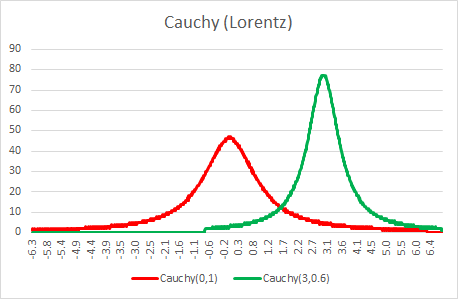
If you like to simulate how particles emanating from a fixed point hit a straight line you can use a Cauchy distribution. This distribution is sometimes called a Lorentz distribution, too. The quotient of two Normal(0,1) distributions also leads to a Cauchy distribution.
Appendix – sbRandCauchy Code
Please read my Disclaimer.
Option Explicit
Const GCPi = 3.14159265358979
Function sbRandCauchy(dLocation As Double, dScale As Double, _
Optional dRandom = 1#) As Double
'Source (EN): https://www.sulprobil.com/sbrandcauchy_en/
'Source (DE): https://www.bplumhoff.de/sbrandcauchy_de/
'(C) (P) by Bernd Plumhoff 03-Nov-2020 PB V0.2
Static bRandomized As Boolean
Dim dRand As Double
If dRandom < 0# Or dRandom > 1# Or dScale <= 0# Then
sbRandCauchy = CVErr(xlErrValue)
Exit Function
End If
If Not bRandomized Then
Randomize
bRandomized = True
End If
If dRandom = 1# Then
dRand = Rnd()
Else
dRand = dRandom
End If
sbRandCauchy = dLocation + dScale * Tan((dRand - 0.5) * GCPi)
End Function