sbNRN (VBA) ·

“If you don’t know where you are going, you might wind up someplace else.” [Yogy Berra]

Abstract

Which rational number is a good proxy of π (3.1415926…)? Enter in cell A1 ‘=pi()', in cell B1 your maximal denominator (for example 10), and in cells C1:D1 ‘=sbNRN(A1,B1)' as array formula (with CTRL + SHIFT + ENTER). You will get in C1:D1 22 and 7. That means: 22/7 is the nearest rational number to π with a denominator not higher than 10. For 1000 in B1 you would get 355/113.

This algorithm does NOT necessarily find the nearest rational number to a given floating point number with a given maximal denominator and a maximal absolute error. The good message is, though, that it would then return a #NUM! error. In this case please try an individual maximal absolute error.

The author’s (Oliver Aberth) original intention was to support exact computation with rational numbers, for example solving a set of linear equations with rational coefficients.

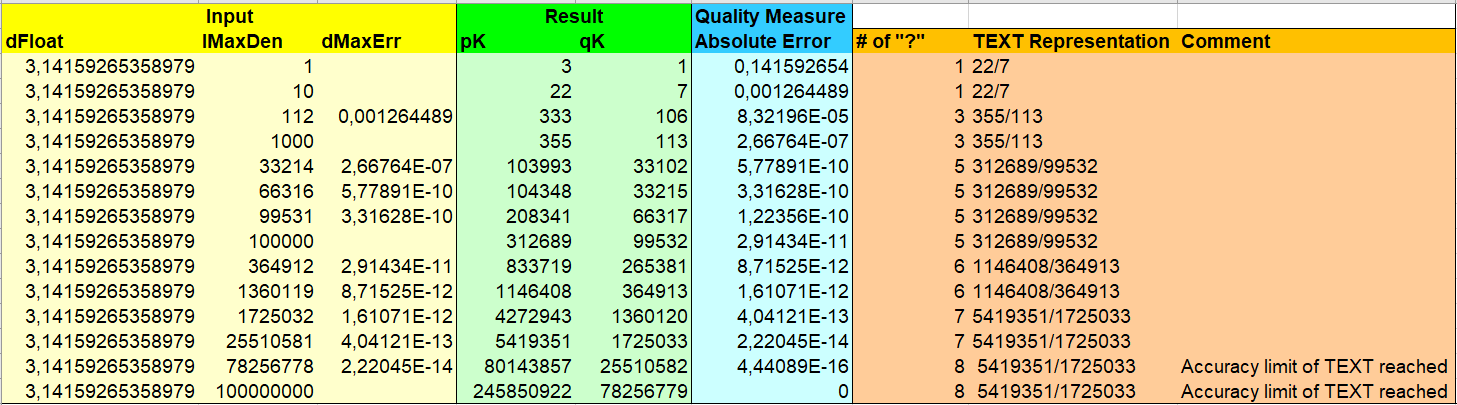
Nearest Rational Number

Note: The last row in this graphic does not tell us that we have successfully squared the circle. We have reached (my) Excel’s limit of accuracy.

The fraction representations of the TEXT function are shown for comparison.
Example: =TEXT(PI(),"?/?") = “22/7”
Microsoft did not extend this representation for its 64-Bit version. It cannot get more accurate than PI() = “5419351/1725033”. With 64-Bit PI() = “245850922/78256779” would be more accurate, but in this case the absolute error is already less than 1e-15, of course.

A simple sample application you find at Quota Change as Fraction.

Calculation Limits

Excel can represent decimal numbers from -9.99999999999999E+307 to 9.99999999999999E+307. Excel’s 64-bit version can use integers of type LongLong from -9223372036854775808 to 9223372036854775807 which is about -1E+10 to 1E+10.

It is obvious that Aberth’s algorithm cannot calculate sufficiently accurate fractions for all available decimal numbers with Excel.

Name

sbNRN - Compute nearest rational number to a given floating point number with a given maximal denominator

Synopsis

sbNRN(dFloat, lMaxDen, [dMaxErr])

Description

sbNRN computes the nearest rational number to a given floating point number dFloat with a given maximal denominator lMaxDen and an optional maximal error dMaxErr.

Options

dFloat - Floating point number for which you want to derive the nearest rational number

lMaxDen - Maximal denominator which you want to allow

dMaxErr - Optional - Maximal absolute error (absolute difference between input float and output rational number) which you want to allow

Excursus

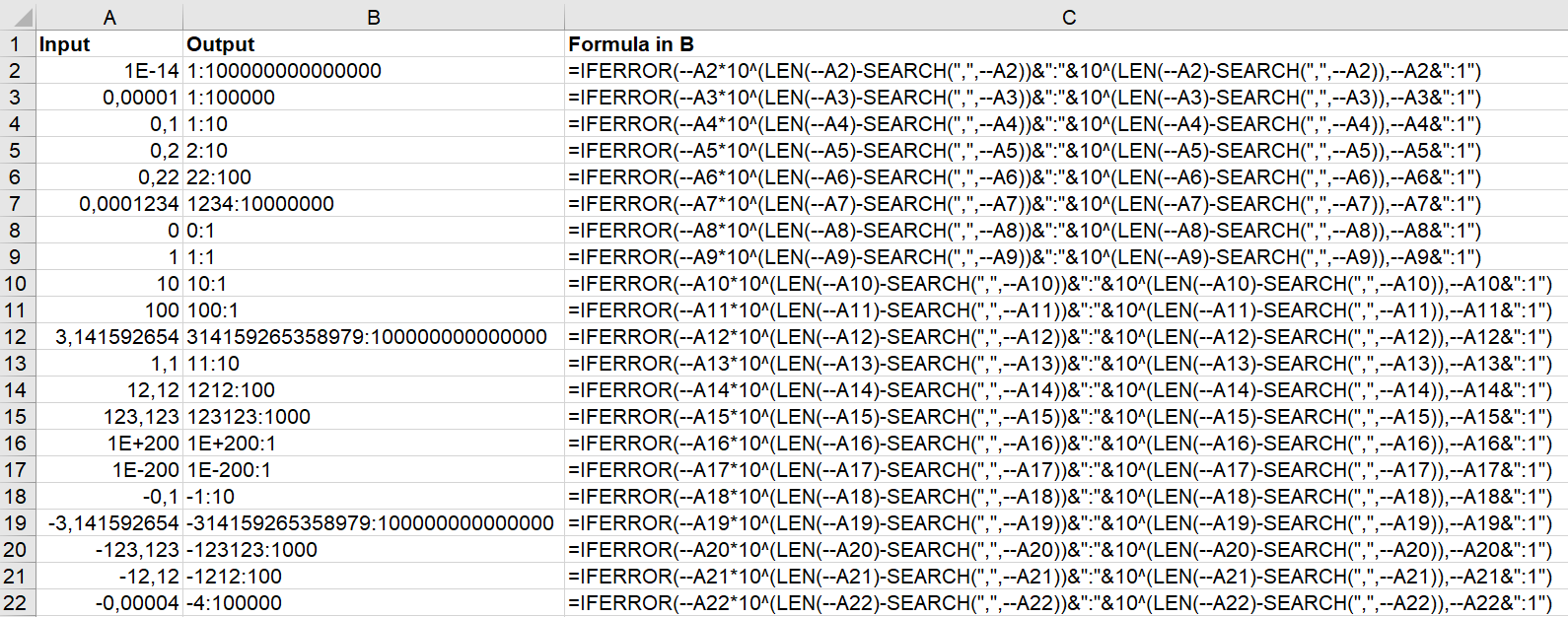
In case you just need the relation to its power of 10, you can use the formula =IFERROR(–A2*10^(LEN(–A2)-SEARCH(",",–A2))&":"&10^(LEN(–A2)-SEARCH(",",–A2)),–A2&":1"):

Relation to Power of 10

Appendix – sbNRN Code

Please read my Disclaimer.

Option Explicit

#If Win64 Then
Function sbNRN(dFloat As Double, lMaxDen As LongLong, _
               Optional dMaxErr As Double = -1#) As Variant
#Else
Function sbNRN(dFloat As Double, lMaxDen As Long, _
               Optional dMaxErr As Double = -1#) As Variant
#End If
'Computes nearest rational number to dFloat with a maximal denominator
'lMaxDen and a maximal absolute error dMaxErr and returns result as a
'variant Nominator / Denominator.
'See: Oliver Aberth, A method for exact computation with rational numbers,
'     JCAM, vol 4, no. 4, 1978
'Source (EN): http://www.sulprobil.com/sbnrn_en/
'Source (DE): http://www.bplumhoff.de/sbnrn_de/
'Bernd Plumhoff V1.21 09-Oct-2020

Dim dB As Double
#If Win64 Then
Dim lA As LongLong, lSgn As LongLong
Dim lP1 As LongLong, lP2 As LongLong, lP3 As LongLong
Dim lQ1 As LongLong, lQ2 As LongLong, lQ3 As LongLong
#Else
Dim lA As Long, lSgn As Long
Dim lP1 As Long, lP2 As Long, lP3 As Long
Dim lQ1 As Long, lQ2 As Long, lQ3 As Long
#End If

If dMaxErr = -1# Then dMaxErr = 1# / (2# * CDbl(lMaxDen) ^ 2#)
lSgn = Sgn(dFloat): dB = Abs(dFloat)
lP1 = 0: lP2 = 1: lQ1 = 1: lQ2 = 0

Do While lMaxDen > lQ2
    lA = Int(dB)
    lP3 = lA * lP2 + lP1: lQ3 = lA * lQ2 + lQ1
#If Win64 Then
    If Abs(dB - CDbl(lA)) < 1# / CLngLng("9223372036854775807") Then
#Else
    If Abs(dB - CDbl(lA)) < 1# / 2147483647# Then
#End If
        Exit Do
    End If
    dB = 1# / (dB - CDbl(lA))
    lP1 = lP2: lP2 = lP3: lQ1 = lQ2: lQ2 = lQ3
Loop

If lQ3 > lMaxDen Then
    lQ3 = lQ2: lP3 = lP2
    If lQ2 > lMaxDen Then
        lQ3 = lQ1: lP3 = lP1
    End If
End If

'If absolute error exceeds 1/2Q^2 then Aberth's lemma p. 286 might not apply.
'But the user can override this and check the result himself.
If Abs(dFloat - lSgn * lP3 / lQ3) > dMaxErr Then
    sbNRN = CVErr(xlErrNum)
Else
    sbNRN = Array(lSgn * lP3, lQ3)
End If

End Function

Download