Abstract
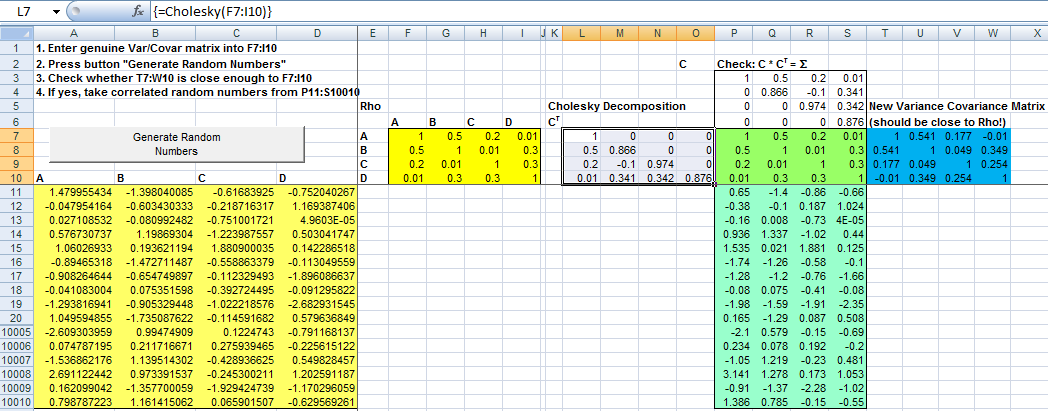
You can generate correlated random variables easily with a Cholesky (pronounce “koleski”) decomposition. I present a simple example here. For the better Iman Conover approach look here.
Appendix – Cholesky Code
Please read my Disclaimer.
Function Cholesky(r As Range) As Variant
'I suggest to use the Cholesky decomposition just for purposes of demonstration.
'Better options are (in this order): tred2, tqli, eigsrt from Numerical Recipes.
'SVD also works but is computationally more expensive by far since it does not
'make use of symmetry.
'(Thanks to my friend and former colleague Glen R.)
'Source (EN): http://www.sulprobil.com/cholesky_en/
'Source (DE): http://www.bplumhoff.de/cholesky_de/
'Bernd Plumhoff 22-Nov-2019 PB V1.0
Dim vA As Variant
Dim d As Double
Dim i As Long, j As Long, k As Long, n As Long
vA = r
n = r.Rows.Count
If n <> r.Columns.Count Then
Cholesky = CVErr(xlErrRef)
Exit Function
End If
ReDim vR(1 To n, 1 To n) As Variant
For j = 1 To n
d = 0#
For k = 1 To j - 1
d = d + vR(j, k) * vR(j, k)
Next k
vR(j, j) = vA(j, j) - d
If vR(j, j) > 0# Then
vR(j, j) = Sqr(vR(j, j))
For i = j + 1 To n
d = 0#
For k = 1 To j - 1
d = d + vR(i, k) * vR(j, k)
Next k
vR(i, j) = (vA(i, j) - d) / vR(j, j)
Next i
Else
'Cannot continue with usual Cholesky
'Fill this column with zeros. Idea: Glen R.
For i = j To n
vR(i, j) = 0#
Next i
End If
Next j
Cholesky = vR
End Function
Download
Please read my Disclaimer.
Cholesky.xlsm [270 KB Excel file, open and use at your own risk]